什么是布隆过滤器

布隆过滤器（Bloom Filter）是 1970 年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都比一般的算法要好的多，缺点是有一定的误识别率和删除困难。

布隆过滤器（Bloom Filter）本质上是由长度为 m 的位向量或位列表（仅包含 0 或 1 位值的列表）组成，最初所有的值均设置为 0，如下图所示。

向布隆过滤器中添加 key 时，会使用多个 hash 函数对 key 进行 hash 运算得到一个整数索引值然后对位数组长度进行取模运算得到一个位置，每个 hash 函数都会算得一个不同的位置，再把位数组的这几个位置都设置为 1 就完成了 add 操作。

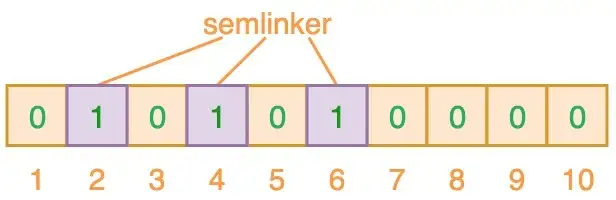
如上图所示，当输入 “semlinker” 时，预设的 3 个哈希函数将输出 2、4、6，我们把相应位置 1。假设另一个输入 ”kakuqo“，哈希函数输出 3、4 和 7。你可能已经注意到，索引位 4 已经被先前的 “semlinker” 标记了。此时，我们已经使用 “semlinker” 和 ”kakuqo“ 两个输入值，填充了位向量。当前位向量的标记状态为：

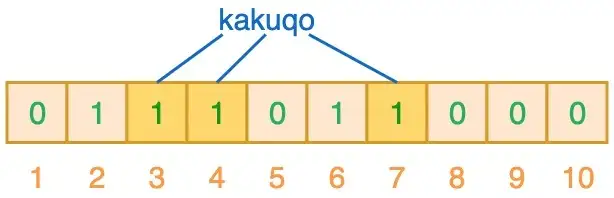
向布隆过滤器查询 key 是否存在时，也会把 hash 的几个位置都算出来，看看位数组中这几个位置是否都为 1，只要有一个位为 0，那么说明布隆过滤器中这个key 不存在。如果都是 1，这并不能说明这个key 就一定存在，只是可能存在，因为这些位被置为 1 可能是因为其它的 key 存在所致。如果这个位数组比较稀疏，这个概率就会很大，如果这个位数组比较拥挤，这个概率就会降低。

也就是说，当布隆过滤器说某个值存在时，这个值可能不存在；当它说不存在时，那就肯定不存在。

我们举个例子，当对值进行搜索时，我们将使用 3 个哈希函数对 ”搜索的值“ 进行哈希运算，并查看其生成的索引值。假设，当我们搜索 ”fullstack“ 时，3 个哈希函数输出的 3 个索引值分别是 2、3 和 7：

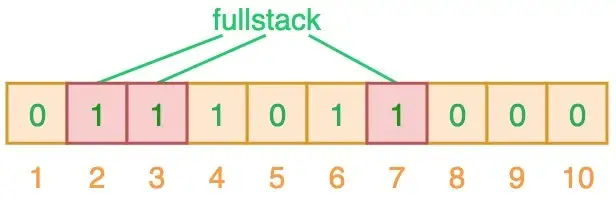
从上图可以看出，相应的索引位都被置为 1，这意味着我们可以说 ”fullstack“ 可能已经插入到集合中。事实上这是误报的情形，产生的原因是由于哈希碰撞导致的巧合而将不同的元素存储在相同的比特位上。

布隆过滤器适用于数据命中不高、 数据相对固定、 实时性低（通常是数据集较大） 的应用场景， 代码维护较为复杂， 但是缓存空间占用很少。

布隆过滤器的优点：

• 时间复杂度低，增加和查询元素的时间复杂为O(N)，（N为哈希函数的个数，通常情况比较小）

• 保密性强，布隆过滤器不存储元素本身

• 存储空间小，如果允许存在一定的误判，布隆过滤器是非常节省空间的（相比其他数据结构如Set集合）

布隆过滤器的缺点：

• 有一定的误判率，但是可以通过调整参数来降低
• 无法获取元素本身
• 很难删除元素

布隆过滤器不能删除删除元素，只能重新构建。

布隆过滤器的使用场景

• 解决Redis缓存穿透问题
• 邮件过滤，使用布隆过滤器来做邮件黑名单过滤
• 对爬虫网址进行过滤，爬过的不再爬
• 解决新闻推荐过的不再推荐(类似抖音刷过的往下滑动不再刷到)
• HBase\RocksDB\LevelDB等数据库内置布隆过滤器，用于判断数据是否存在，可以减少数据库的IO请求

布隆过滤器的原理

数据结构

布隆过滤器它实际上是一个很长的二进制向量和一系列随机映射函数。以Redis中的布隆过滤器实现为例，Redis中的布隆过滤器底层是一个大型位数组（二进制数组）+多个无偏hash函数。

一个大型位数组（二进制数组）：

多个无偏hash函数： 无偏hash函数就是能把元素的hash值计算的比较均匀的hash函数，能使得计算后的元素下标比较均匀的映射到位数组中。

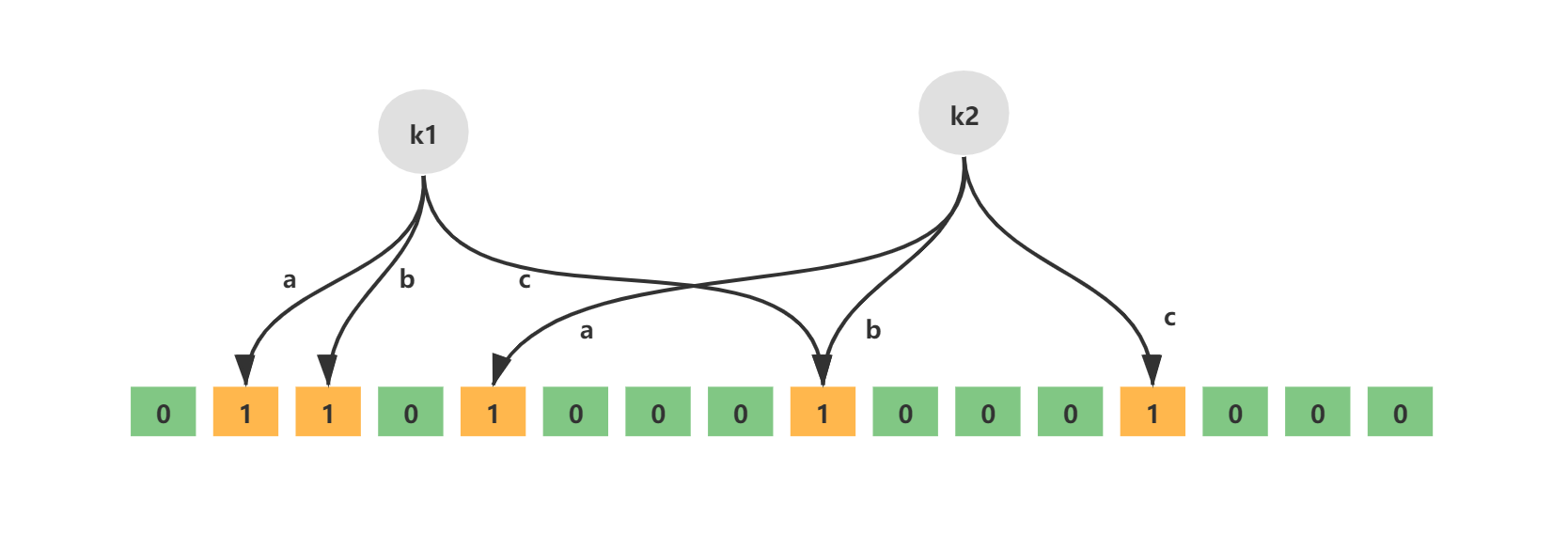
如下就是一个简单的布隆过滤器示意图，其中k1、k2代表增加的元素，a、b、c即为无偏hash函数，最下层则为二进制数组。

空间计算

在布隆过滤器增加元素之前，首先需要初始化布隆过滤器的空间，也就是上面说的二进制数组，除此之外还需要计算无偏hash函数的个数。布隆过滤器提供了两个参数，分别是预计加入元素的大小n，运行的错误率f。布隆过滤器中有算法根据这两个参数会计算出二进制数组的大小l，以及无偏hash函数的个数k。 它们之间的关系比较简单：

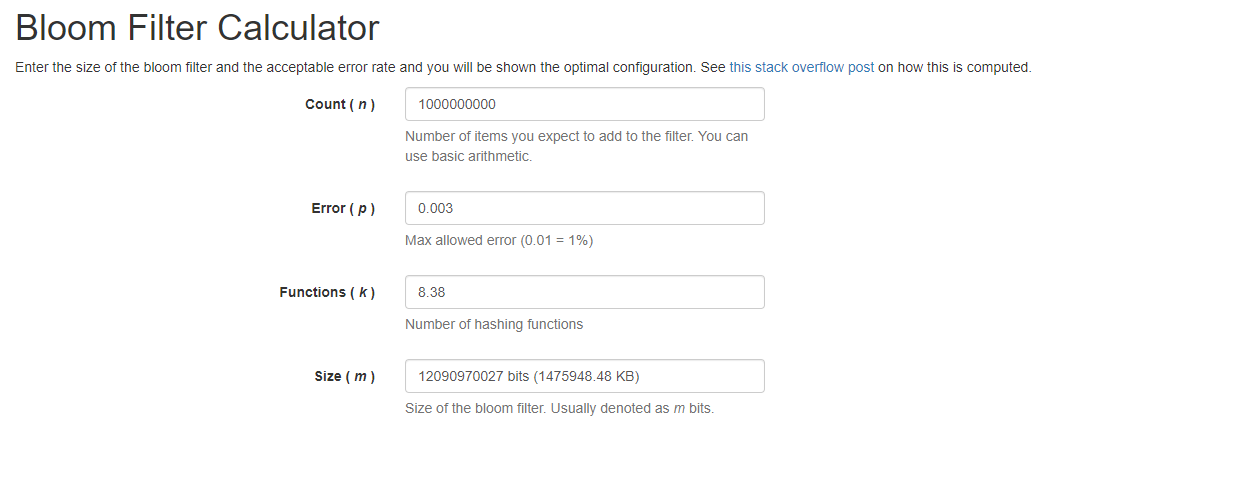
错误率越低，位数组越长，控件占用较大 错误率越低，无偏hash函数越多，计算耗时较长 如下地址是一个免费的在线布隆过滤器在线计算的网址：

https://krisives.github.io/bloom-calculator/

增加元素

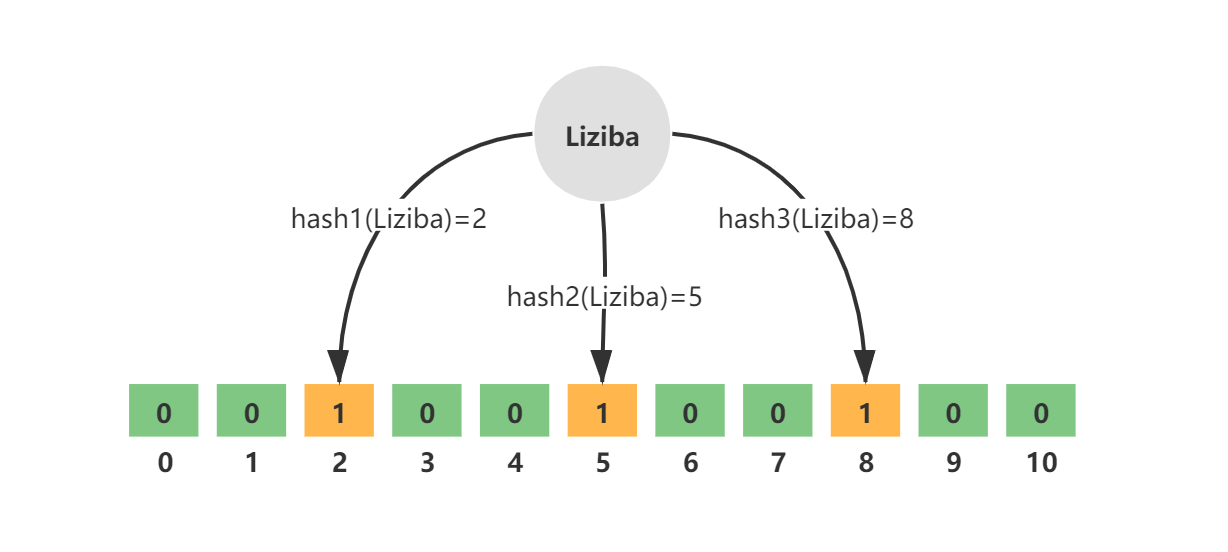
往布隆过滤器增加元素，添加的key需要根据k个无偏hash函数计算得到多个hash值，然后对数组长度进行取模得到数组下标的位置，然后将对应数组下标的位置的值置为1

通过k个无偏hash函数计算得到k个hash值 依次取模数组长度，得到数组索引 将计算得到的数组索引下标位置数据修改为1 例如，key = Liziba，无偏hash函数的个数k=3，分别为hash1、hash2、hash3。三个hash函数计算后得到三个数组下标值，并将其值修改为1. 如图所示：

查询元素

布隆过滤器最大的用处就在于判断某样东西一定不存在或者可能存在，而这个就是查询元素的结果。其查询元素的过程如下：

• 通过k个无偏hash函数计算得到k个hash值

• 依次取模数组长度，得到数组索引

• 判断索引处的值是否全部为1，如果全部为1则存在（这种存在可能是误判），如果存在一个0则必定不存在

关于误判，其实非常好理解，hash函数在怎么好，也无法完全避免hash冲突，也就是说可能会存在多个元素计算的hash值是相同的，那么它们取模数组长度后的到的数组索引也是相同的，这就是误判的原因。例如李子捌和李子柒的hash值取模后得到的数组索引都是1，但其实这里只有李子捌，如果此时判断李子柒在不在这里，误判就出现啦！因此布隆过滤器最大的缺点误判只要知道其判断元素是否存在的原理就很容易明白了！

删除元素

布隆过滤器对元素的删除不太支持，目前有一些变形的特定布隆过滤器支持元素的删除！关于为什么对删除不太支持，其实也非常好理解，hash冲突必然存在，可能会误删！

Redis集成布隆过滤器

在面试的时候经常会被问到缓存穿透怎么解决。这时候就可以先把所有数据加载到布隆过滤器中，查询的时候先在布隆过滤器里过滤，布隆过滤器如果返回没有，这个数据就一定没有，可以屏蔽到一些无效的请求。

引入依赖

<dependency>
    <groupId>org.redisson</groupId>
    <artifactId>redisson</artifactId>
    <version>3.6.5</version>
</dependency>

测试案例：

 public static void main(String[] args) {
        Config config = new Config();
        config.useSingleServer().setAddress("redis://ip:port").setPassword("pwd");
        //构造Redisson
        RedissonClient redisson = Redisson.create(config);

        RBloomFilter<String> bloomFilter = redisson.getBloomFilter("nameList");
        //初始化布隆过滤器：预计元素为100000000L,误差率为3%,根据这两个参数会计算出底层的bit数组大小
        bloomFilter.tryInit(100000000L,0.03);
        //插入到布隆过滤器中
        bloomFilter.add("zhangfei");

        //判断下面号码是否在布隆过滤器中
        System.out.println(bloomFilter.contains("guanyu"));//false
        System.out.println(bloomFilter.contains("liubei"));//false
        System.out.println(bloomFilter.contains("zhangfei"));//true
    }

我们再来看下误判：

        /** 预计插入的数据 */
        Integer expectedInsertions = 10000;
        /** 误判率 */
        Double fpp = 0.01;
        // 初始化布隆过滤器
        RedissonClient client = Redisson.create(config);
        RBloomFilter<Object> bloomFilter2 = client.getBloomFilter("user");
        bloomFilter2.tryInit(expectedInsertions, fpp);

        // 布隆过滤器增加元素
        for (Integer i = 0; i < expectedInsertions; i++) {
            bloomFilter2.add(i);
        }

        // 统计元素
        int count = 0;
        for (int i = expectedInsertions; i < expectedInsertions*2; i++) {
            if (bloomFilter2.contains(i)) {
                count++;
            }
        }
        System.out.println("误判次数" + count); // 255

总结

本文主要讲述了布隆过滤器的原理，以及在Redis中怎么使用布隆过滤器。